The most fun you can have on the Internet is to find a beautiful, succinct argument with a conclusion so unexpected it seems like magic. For today’s fun, I am indebted to Michael Lugo, at God Plays Dice.
Lugo’s original post is so good it seems almost superflous to paraphrase it, but I can’t resist the temptation.
Drill a tunnel through the earth, from anywhere to anywhere — New York to Maine, or New York to Australia, or wherever else you like. Like so:
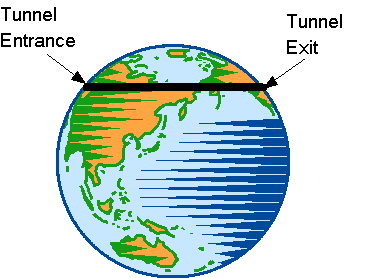
Now drop the object of your choice (Lugo suggests a burrito, but you might prefer a gravity-driven train) into the tunnel entrance and wait till it comes out the other side. It’s a standard calculus problem to calculate how long you’ll have to wait: The answer is 42 minutes, regardless of the length of the tunnel. I’m sure I once found it surprising that the tunnel length doesn’t matter, but I’ve known it long enough that I now take it in stride. So that’s not how Lugo surprised me.
The surprise is that if you change the size of the earth (while maintaining its density), the answer is still 42 minutes. Whether the earth is the size of a pea or the size of the solar system, it’s a 42 minute trip from one end of the tunnel to the other. (We’re — quite reasonably — ignoring the effects of relativity here. For an earth that was half the size of the universe, we’d have to make some corrections.)
Why so? You could, of course, discover this through a direct calculation. But Lugo provides a much slicker argument, namely:
Once you know that the travel time is independent of the tunnel length, it’s clear there are only three things it can depend on: The earth’s density, its radius, and the gravitational constant. Neither density nor radius have anything to do with time, so we’re really going to have to use that gravitational constant, which is measured in units of
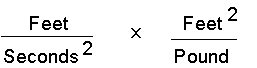
(The first factor is the 32 feet per second squared that you learned about in elementary school; the second factor depends on distance from the center of the earth and the mass of the earth, neither of which varies in those elementary school problems, so it’s never explicitly mentioned.)
If you multiply that gravitational constant by density (which is pounds per cubic foot), you’ll get a bunch of cancellation, leaving you with
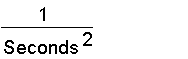
Now you’ve got something that depends only on time! To turn this into an actual number of seconds, you can just invert it and take the square root. At that point, you’re done! (Except maybe for multiplying by some dimensionless constant.) Any attempt to bring the radius of the earth into the formula is going to introduce units of length, which have no business popping up in a formula for time. Therefore the earth’s radius must be irrelevant.
Isn’t that cool? And amazing?
(And yes, there are hidden assumptions, e.g. that the solution must be not just a function of mass, length and the gravitational constant, but a rational function — so this is not quite a proof, but a highly convincing heuristic argument that does give the correct answer. That, I think, in no way detracts from its coolness.)
Lugo’s post is both more concise and more carefully worded, but I thought this slightly longer and less formal version might be helpful to at least a reader or two. Besides, I felt like writing it.
Do you have an equally amazing argument to share?